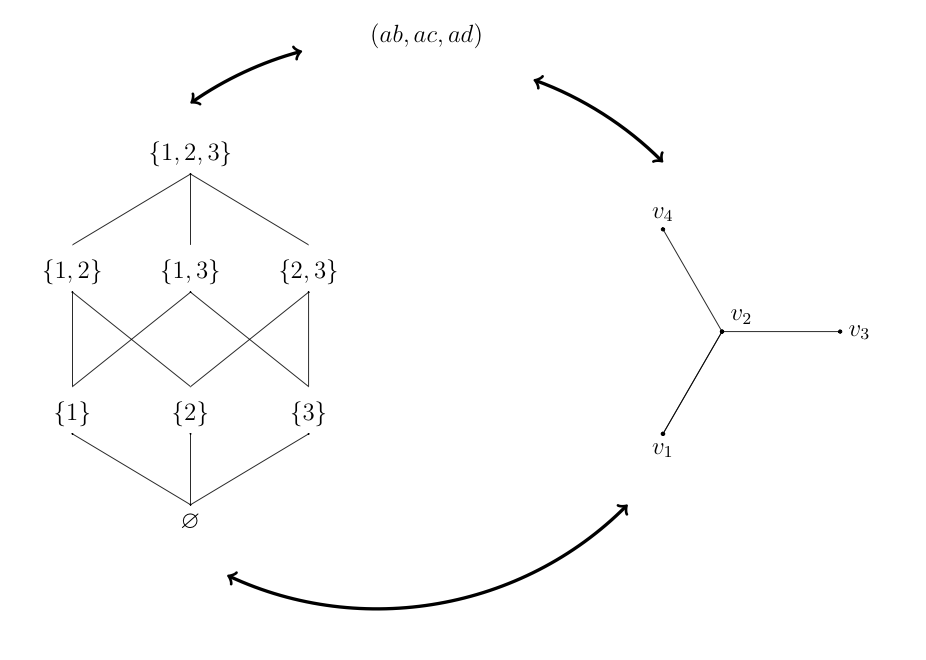
In this talk I will describe the process of associating a finite graph to a set of degree 2 monomials and to a finite atomic lattice. Characteristics of these combinatorially rich objects influence the structure of their associated counterparts and give rise to many (unanswered) questions. I will give classification results obtained by my former undergraduate student Andrea Heyman in the case when the graph in question is a galaxy (disjoint union of stars). This combinatorial result has a commutative algebra interpretation in my research area of free resolutions of monomial ideals. The talk will be self-contained, I will define all relevant combinatorial objects and provide illustrative examples.
